About a third of the earth’s surface is covered by land. More than a third of the land surface is agricultural area (pastures, acreage) and one third is covered by forests. Plants and crops substantially influence the nutrient balance in near-surface soil layer (in the ‘vadose zone’). They play a crucial role for the local water budget and water exchange between soil and atmosphere. Water transpires—particularly during the day with the help of the sun—from small vents in the plant’s leaves. The transpiration causes a suction effect which drives water into the roots and upwards through a vascular system (the root xylem) all the way to the leaves. Both soil and roots are porous media! The appearance and structure of the root system differs between plant species and changes with environmental factors (e.g. soil water content).
Some plants exude a gel-like substance which alters the hydraulic properties of the soil and enables the plant to take up water from very dry soil. Fine root hairs on the surface of roots are assumed to play an important role for water uptake. Complex root architectures can lead to a local redistribution of the available water. Such process cannot only be observed in experiments but can also be analyzed with computer simulations. For example, the complex interaction between direct evaporation from soil and transpiration from plants can be investigated by using simulations. Here, simulations have a crucial advantage over experiments. Processes can simply be switched on and off. This allows to investigate a process and its effect in isolation as well as in interaction with other processes. On the basis of investigations with detailed models of one or a small number of plants, it can be decided whether such processes can be neglected or must be considered in large-scale simulation such as climate models.
At the University of Stuttgart, we work—together with colleagues at Forschungszentrum Jülich— on the development of novel computer models for water and nutrient transport, root-soil interaction and root growth. These models are innovative tools for the assessment of scientific theories and hypotheses about water transport in soil. However, this is only possible under the premise that these models accurately represent all considered processes. For instance, most state-of-the-art models overestimate root water uptake in dry soils for a given atmospheric pressure. We analyze computer models and create improved model which address known shortcomings.
Credits: University of Stuttgart / Timo Koch
Fractures are features which are commonly found in geological materials, and they can have a strong impact on their hydraulic and mechanical properties. For example, highly conductive fractures in a low-permeable rock can act as preferential flowpaths along which rapid fluid flow can occur. Besides that, the fractures provide interfacial areas for the transfer of mass and/or heat between the fractures and the surrounding rock. Several geotechnical engineering applications make use of this fact, as for example geothermal energy or unconventional shale gas production techniques.
The motivation for the development of the model presented here originates from a project related to underground radioactive waste storage. One approach is storing the waste inside tunnel systems that are excavated within low-permeable clay formations, which act as barriers for flow and transport of potentially radioactive components over large time scales. Transport away from the emplacement tunnels could be driven by the pressure increase that is expected to occur due to the release of hydrogen gas as a consequence of the anaerobic corrosion of the metal canisters. Besides this, the excavation of the tunnels leads to the creation of fractures in the near vicinity of the emplacement tunnels.
The scientific question that arises is how the fractures present in the surroundings of the tunnels influence the hydraulic properties of the clay rock. Clay rock is relatively soft, which is why the current hypothesis is that the dilation of the present fractures can help to reduce the pressure build-up inside the emplacement tunnels. To this end, experimental studies on cylindrical rock samples taken from the surrounding clay rock are envisaged, with which the dilation of the fractures as function of the pressure increase is to be quantified.
The model that is presented here was designed to provide a tool with the help of which the experimental results can be better interpreted, and which allows for studying the hydraulic properties of a number of synthetically generated rock samples and fracture networks. In experimental studies, this would involve very large technical and financial efforts. The model considers a poroelastic rock matrix, that is, the interaction between the flow through and the deformation of the rock sample is taken into account, and the rock is described by means of a linear elastic material law. Besides this, flow along the fractures is considered, where the fractures are modeled as two-dimensional planes as the fracture apertures are typically very small in comparison the extent of the samples. The aperture is then a variable defined on the fracture planes and is a function of the deformation of the medium. This way, the influence of the deformation on the hydraulic properties of the fractures, and in turn on the hydraulic properties of the entire sample, is captured.
Credits: University of Stuttgart / Dennis Gläser
Magnetic resonance imaging (MRI) is an immensely important and versatile imaging technique used for medical imaging. The technique is based on the nuclear magnetic resonance of hydrogen atoms to radio frequency signals in strong magnetic fields. MRI avoids damaging radiation (e.g. X-rays) and is usually considered non-invasive. MRI of the brain is, for example, used in the diagnosis and therapy monitoring of brain tumors, in the analysis of neurodegenerative diseases such as Alzheimer’s or Parkinson’s disease, and diseases of the central nervous system, such as multiple sclerosis. In a variant of MRI called perfusion MRI, a contrast agent is injected into the blood stream and a sequence of MR images is taken to observe the fate of this contrast agent.
Why is it important that the brain is a porous medium?
Like most biological soft tissues, brain tissue consists of a mixture of cells, fibres, and fluid within the cells and the interstitial space (pore space). Cells are supplied by blood vessels with oxygen and nutrients. The blood vessels also consist of cells and blood is a mixture of fluid and various cells. This complex tissue architecture complicates the interpretation of the MRI images.
How can computer simulations help?
Computer models are the basis for the image post-processing done for perfusion MRI data. The model simulates both contrast agent perfusion and the resulting MRI signal and compares the result with the data. Hereby, certain properties of the brain tissue can be inferred. For example, the blood volume fraction can be estimated—an important biomarker for tumors, but equally important to assess the possible damage after a stroke. Simple simulations only take seconds and thus immediately provide important additional informations to medical doctors for decision making.
At the University of Stuttgart, researchers develop novel simulation techniques with the goal of extracting further information from MRI data. Using computer simulations, they try to better understand how contrast agent spreads in brain tissue and how different properties of the tissue influence MRT data.
Credits: University of Stuttgart / Timo Koch
Pretty Porous
01
01
Simulation gallery
Simulation gallery
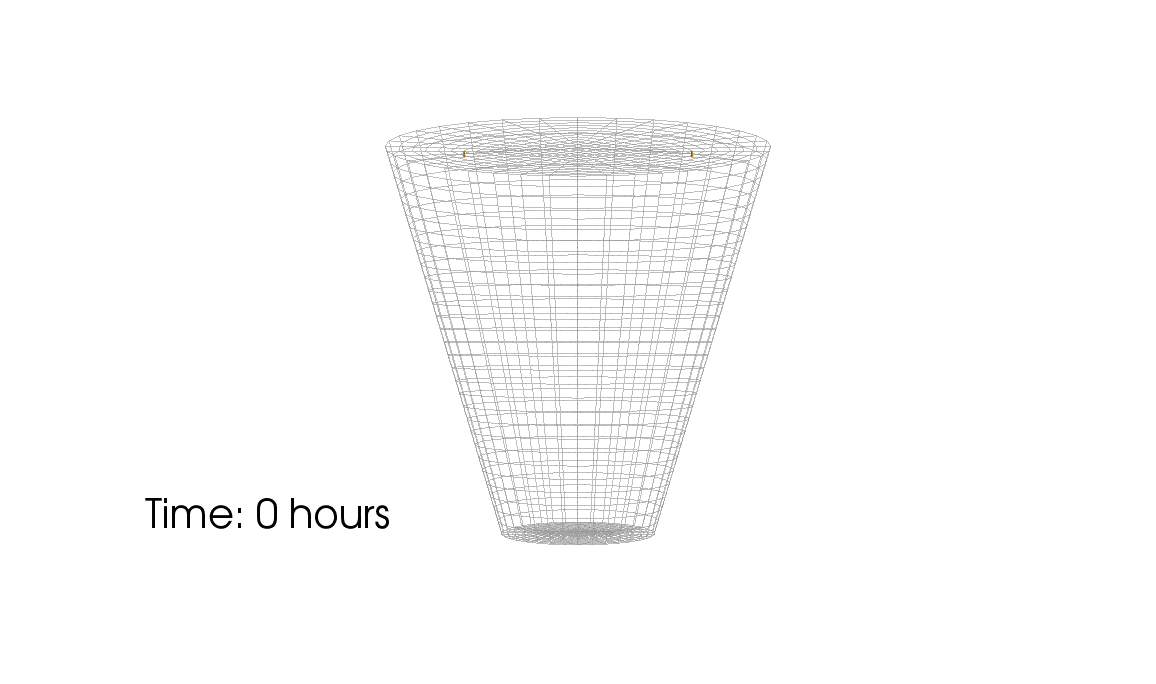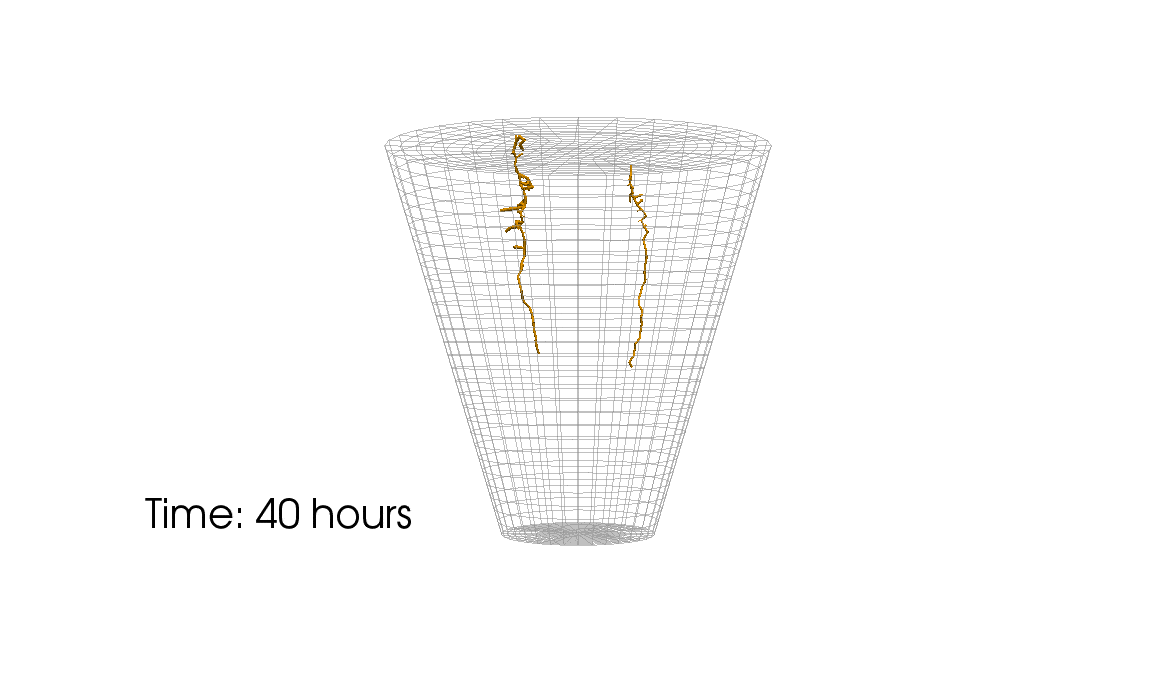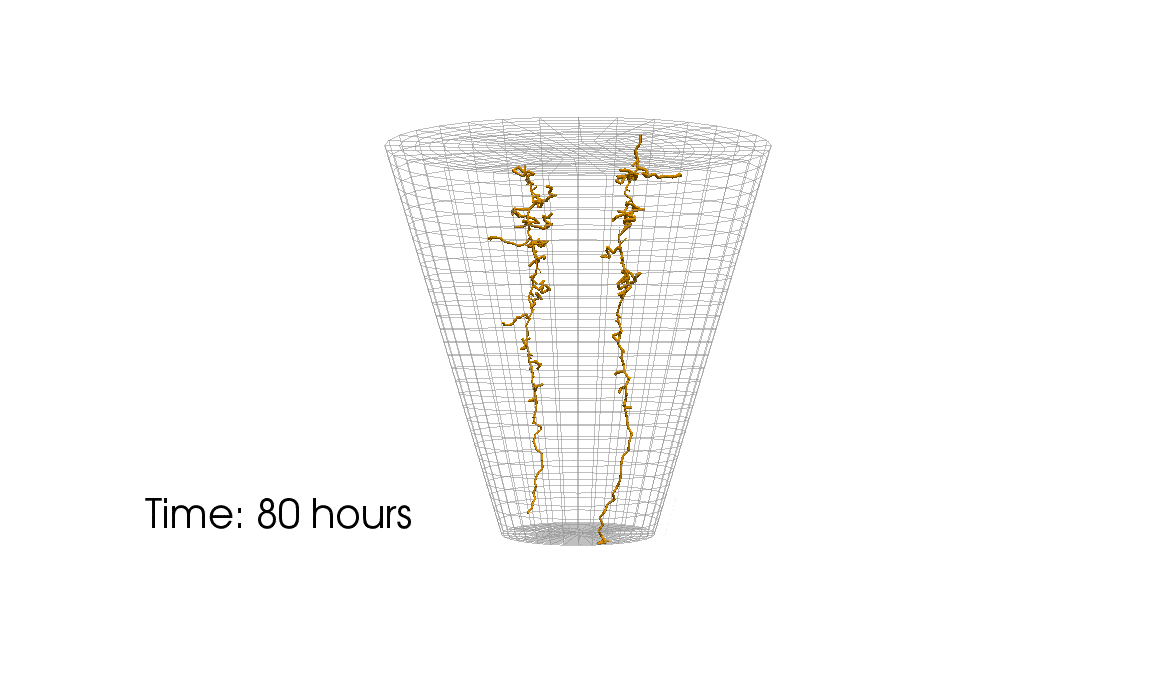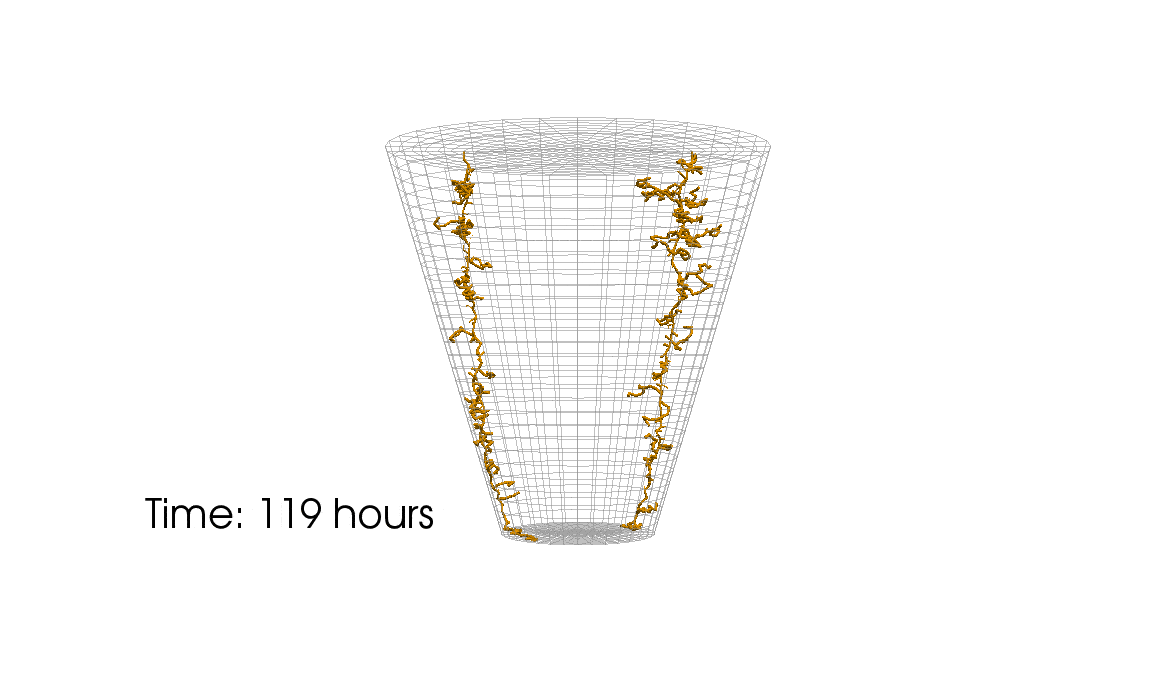
1: Root water uptake by young, growing root systems
This simulation shows the growing root systems of two young plants. The plants take up water from the soil in a plant pot. The soil eventually dries out.
Model: soil and root
Simulation: water transport and root growth
Roots are visualized by brown tube segments. Blue soil corresponds to high water content, brown soil means low water content.
In-depth text
Credits: University of Stuttgart / Timo Koch

Credits: University of Stuttgart / Timo Koch
2: Flow through rock with fractures
This simulation shows the pressure-induced flow of oil through a cylindrical rock sample, in which elliptical fractures are contained. The pressure changes caused by the injection lead to the dilation of the fractures.
Model: porous rock and fractures
Simulation: flow and deformation
The rock is depicted in gray, and the blue region shows until which point the oil has been transported through the sample. The arrows show the velocities of oil within the sample and the deformation of the sample is strongly exaggerated in this visualization.
In-depth text

Credits: University of Stuttgart / Dennis Gläser
3: Contrast agent perfusion in capillaries and embedding tissue
This simulation shows contrast agent transport in the smallest blood vessels (microcirculation). Blood is simplified as a fluid without particles. The cell content is accounted for by an increased flow resistance. The porous tissue surrounding the blood vessels is described by an average description. This means that individual pores between cells are not visible.
Model: brain tissue and capillaries
Simulation: blood flow and contrast agent transport
The capillary network is taken from a rat brain and represents all blood vessels contained in a 1mm by 1mm by 2mm tissue sample. The contrast agent is visualized as a black cloud. Contrast agent leakage is restricted to the middle of the domain. Leaked contrast agent has orange color.
In-depth text
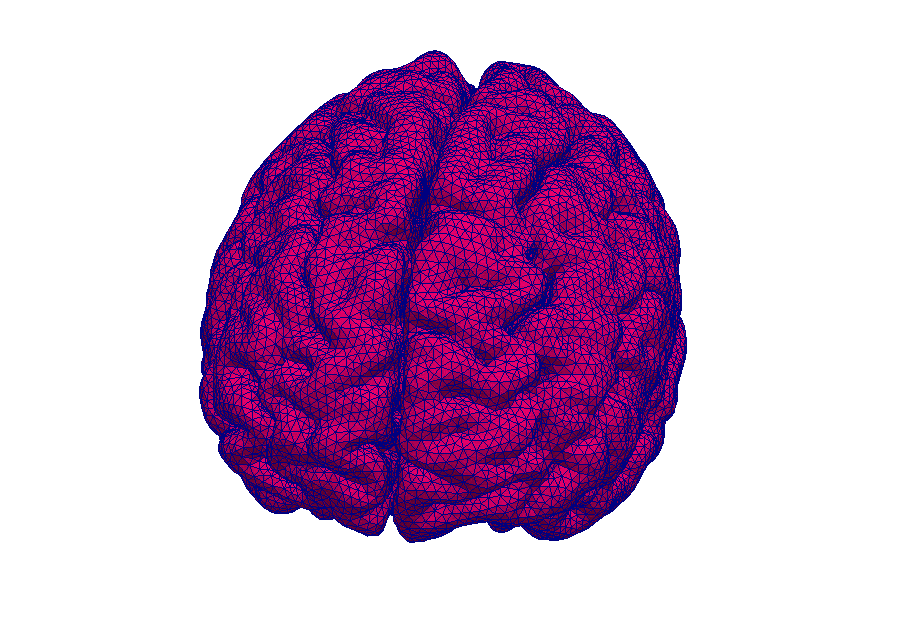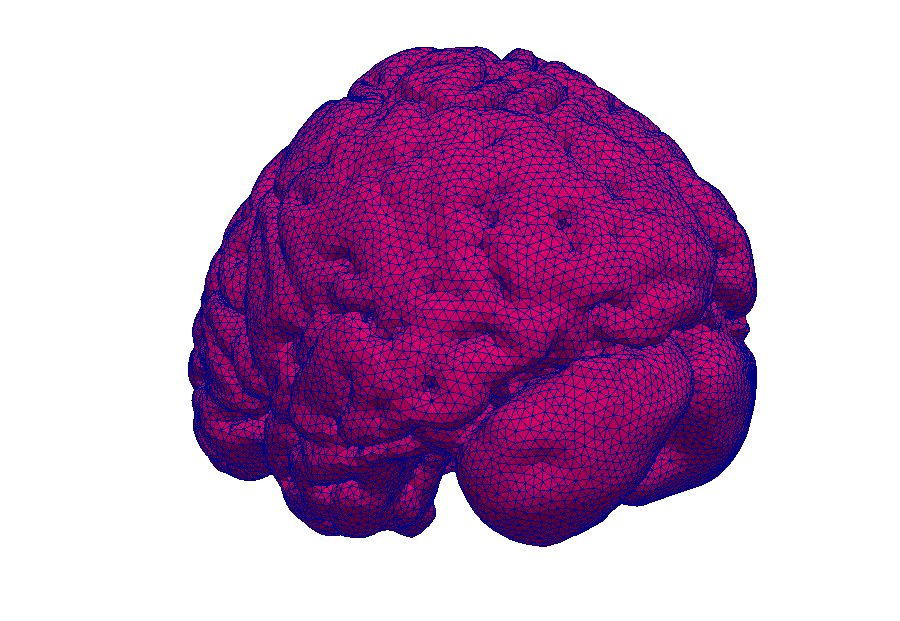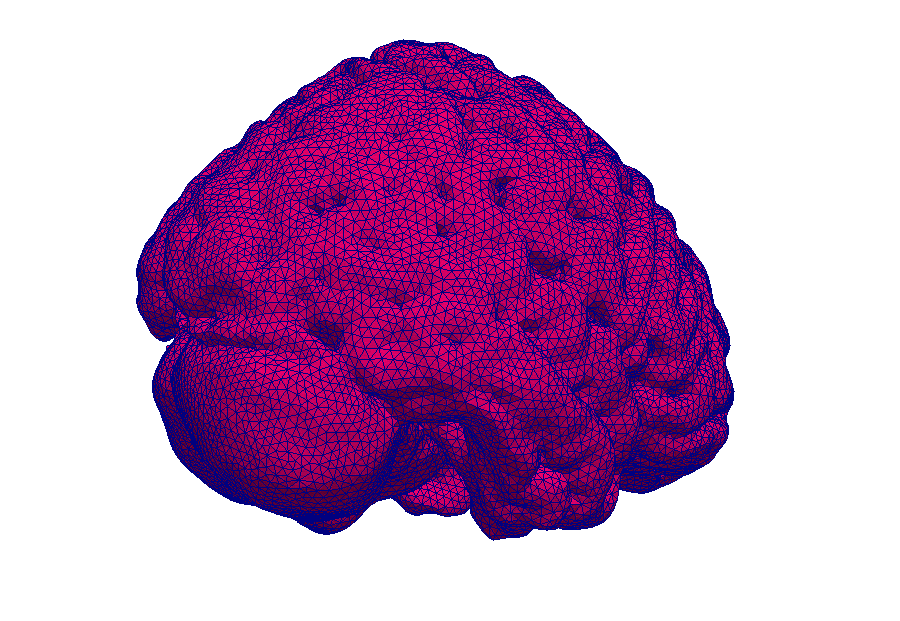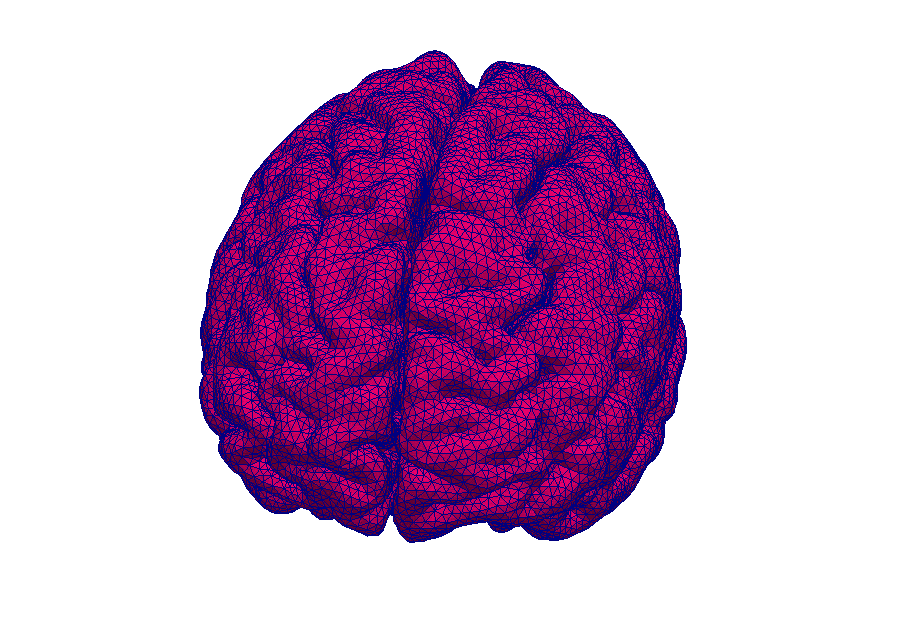
Credits: Timo Koch, University of Stuttgart

Credits: Timo Koch, University of Stuttgart